본문 바로가기
카테고리 없음

연결 리스트의 사이클 탐지 (Floyd's Tortoise and Hare)

by kguidebook0001 2026. 2. 1.

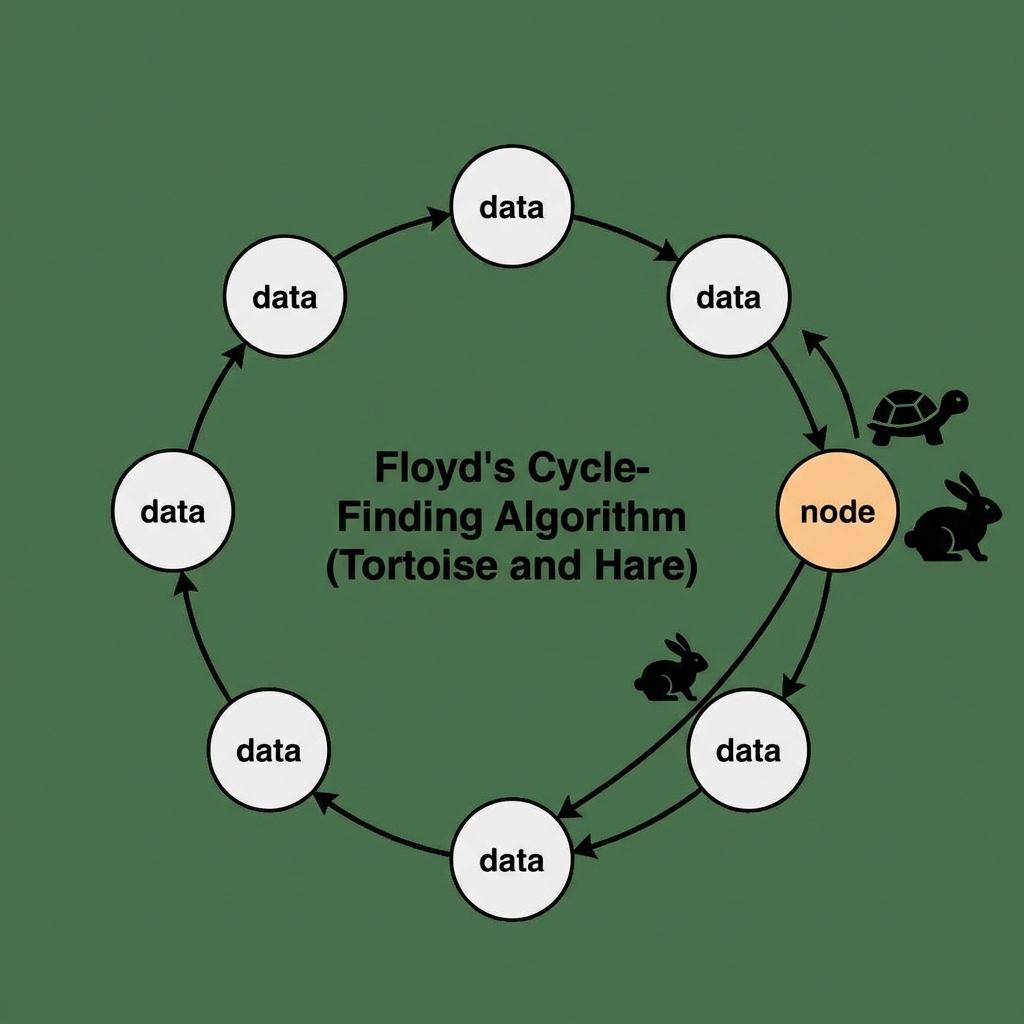
연결 리스트(Linked List)를 다루다 보면 가장 치명적인 버그 중 하나인 '무한 루프(Infinite Loop)', 즉 사이클(Cycle) 문제에 직면하게 됩니다. 리스트의 마지막 노드가 NULL이 아닌 이전의 특정 노드를 다시 가리키게 되면, 프로그램은 영원히 종료되지 않고 시스템 자원을 고갈시키게 됩니다. 이를 방지하기 위해 사이클 존재 여부를 판별해야 하는데, 단순히 방문한 노드를 기록하는 방식(Hash Set)은 O(n)의 추가 메모리를 소모합니다. 오늘은 추가 메모리를 거의 사용하지 않고(O(1)), 속도는 매우 빠른 '플로이드의 토끼와 거북이 알고리즘(Floyd's Tortoise and Hare)'의 원리와 구현 방법을 심층 분석합니다.

1. 알고리즘의 핵심 원리: 속도 차이를 이용한 탐지

플로이드의 사이클 탐지 알고리즘은 '서로 다른 속도로 움직이는 두 개의 포인터'를 사용한다는 점에서 착안하여 '토끼와 거북이'라는 별칭이 붙었습니다. 원리는 직관적입니다. 트랙(순환 코스)에서 토끼(빠른 포인터)와 거북이(느린 포인터)가 동시에 출발한다면, 언젠가는 토끼가 거북이를 뒤에서 따라잡아 만나는 지점이 생긴다는 것입니다.

1-1. 두 개의 포인터 (Two Pointers) 전략

이 알고리즘은 두 개의 포인터를 사용하여 리스트를 순회합니다.

  • Slow Pointer (거북이): 한 번에 1칸씩 이동합니다. (`slow = slow.next`)
  • Fast Pointer (토끼): 한 번에 2칸씩 이동합니다. (`fast = fast.next.next`)

1-2. 만남(Meeting)의 수학적 의미

만약 연결 리스트에 사이클이 없다면, Fast Pointer가 먼저 리스트의 끝(`NULL`)에 도달하여 탐색이 종료됩니다. 반대로 사이클이 있다면, Fast Pointer는 사이클 내부를 계속 돌게 되고, 결국 뒤따라온 Slow Pointer와 반드시 만나게 됩니다. 이때 두 포인터 사이의 거리는 매 스텝마다 1씩 줄어들기 때문에, 영원히 엇갈리지 않고 만나는 것이 수학적으로 보장됩니다.

2. 시간 및 공간 복잡도 분석

이 알고리즘이 현업과 코딩 테스트(LeetCode 등)에서 표준으로 자리 잡은 이유는 압도적인 효율성 때문입니다.

2-1. 공간 복잡도: O(1)

가장 큰 장점입니다. 별도의 해시 셋(Hash Set)이나 배열을 만들어 방문 기록을 저장할 필요 없이, 오직 두 개의 포인터 변수만 사용하므로 메모리 사용량이 상수(Constant)입니다.

2-2. 시간 복잡도: O(n)

사이클이 없는 부분의 길이를 L, 사이클의 길이를 C라고 할 때, 최악의 경우라도 포인터는 리스트를 몇 바퀴 이상 돌지 않습니다. 따라서 리스트의 노드 개수(n)에 비례하는 선형 시간 복잡도를 가집니다.

3. 파이썬(Python) 구현 코드 및 상세 해설

다음은 실제 알고리즘을 구현한 파이썬 코드입니다. 예외 처리(Edge Case) 부분이 중요합니다.


class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution:
    def hasCycle(self, head: ListNode) -> bool:
        # 예외 처리: 리스트가 비어있거나 노드가 하나뿐인 경우 사이클 불가
        if not head or not head.next:
            return False
        
        slow = head
        fast = head
        
        # Fast 포인터가 끝에 도달할 때까지 반복
        while fast and fast.next:
            slow = slow.next          # 거북이: 1칸 이동
            fast = fast.next.next     # 토끼: 2칸 이동
            
            # 두 포인터가 만났다면 사이클 존재
            if slow == fast:
                return True
        
        # 루프를 탈출했다면 끝(NULL)에 도달한 것이므로 사이클 없음
        return False

4. 심화: 사이클의 시작 지점 찾기 (Cycle Start Node)

단순히 사이클의 유무만 판단하는 것을 넘어, "정확히 어느 노드부터 사이클이 시작되는가?"를 묻는 문제도 자주 출제됩니다. 이 또한 플로이드 알고리즘의 확장으로 해결 가능합니다.

해결 로직:

  1. 토끼와 거북이가 만난 지점에서 멈춥니다.
  2. 거북이(Slow)를 다시 헤드(Head)로 돌려보냅니다. 토끼(Fast)는 만난 지점에 그대로 둡니다.
  3. 이제부터 두 포인터 모두 1칸씩 이동시킵니다.
  4. 두 포인터가 다시 만나는 지점이 바로 사이클의 시작 노드입니다.
[핵심 요약 : 플로이드의 사이클 탐지]
1. 원리: 속도가 다른 두 포인터(Fast: 2칸, Slow: 1칸)가 만나는지 확인하여 사이클을 감지합니다.
2. 효율성: 해시 셋을 사용하는 방식(공간 O(n))과 달리, 공간 복잡도 O(1)로 메모리를 최적화할 수 있습니다.
3. 확장: 사이클 유무뿐만 아니라, 추가 로직을 통해 사이클의 진입점까지 정확히 찾아낼 수 있습니다.

티스토리툴바