본문 바로가기
카테고리 없음

우선순위 큐(Priority Queue) 개념잡기 (힙과의 관계)

by kguidebook0001 2026. 1. 31.

 

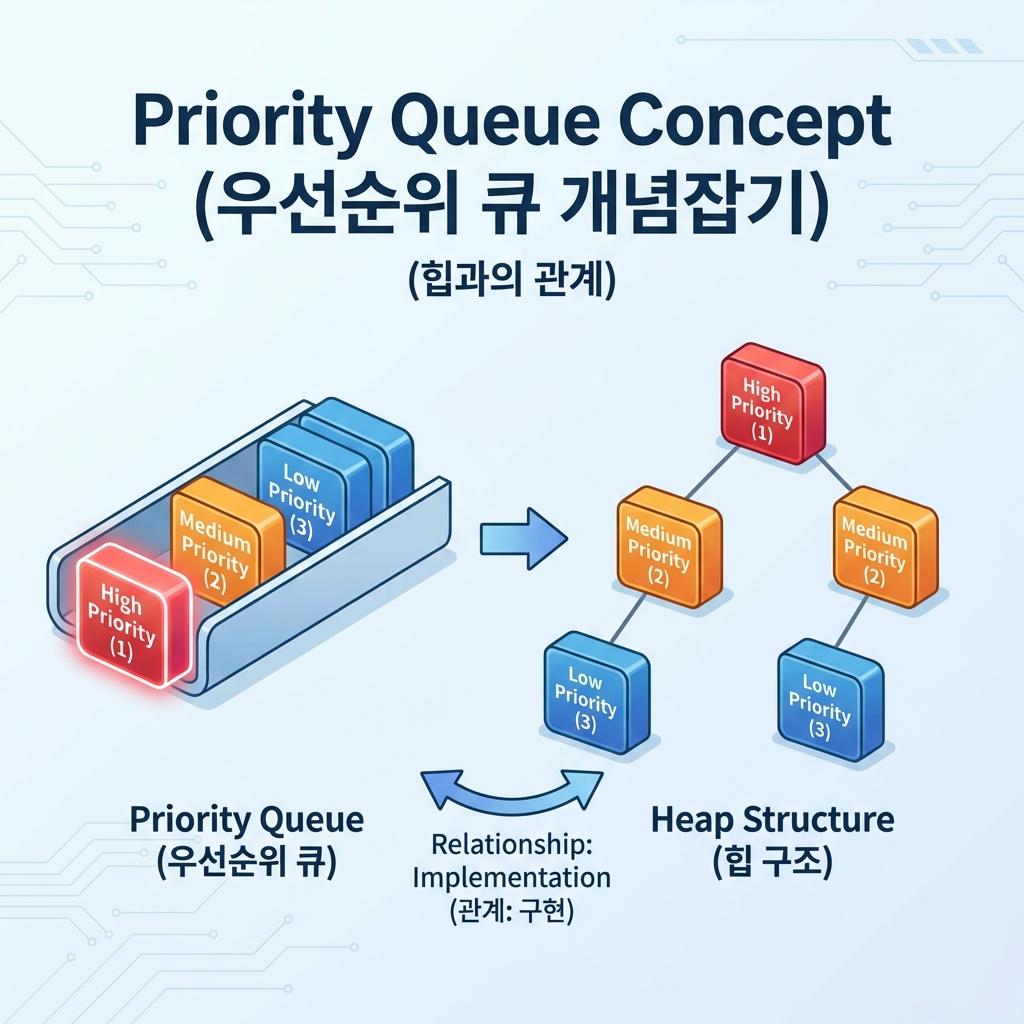
컴퓨터 과학과 시스템 엔지니어링 분야에서 데이터의 처리 순서는 시스템의 효율성을 결정짓는 가장 중요한 요소 중 하나입니다. 일반적으로 사용하는 큐(Queue)는 먼저 들어온 데이터가 먼저 나가는 선입선출(FIFO) 방식을 따르지만, 현실 세계의 문제 해결 과정에서는 '순서'보다 '중요도'가 앞서는 경우가 빈번합니다. 예를 들어, 응급실 환자 분류(Triage)나 운영체제의 프로세스 스케줄링이 그렇습니다. 이러한 요구사항을 충족하기 위해 등장한 자료구조가 바로 우선순위 큐(Priority Queue)입니다. 이 글에서는 우선순위 큐의 개념을 명확히 정의하고, 왜 이 자료구조가 필연적으로 힙(Heap)과 연결될 수밖에 없는지, 그 기술적 인과관계를 심층 분석합니다.

1. 우선순위 큐(Priority Queue)의 정의와 필요성

우선순위 큐는 데이터가 들어온 시점(Time)과 무관하게, 각 데이터가 가진 우선순위(Priority)에 따라 나가는 순서가 결정되는 추상 자료형(ADT)입니다. 일반적인 스택(Stack)이나 큐(Queue)가 데이터의 입출력 순서를 기계적으로 고정했다면, 우선순위 큐는 데이터의 '가치'를 판단하여 유연하게 처리 순서를 조정합니다.

1-1. 동작 메커니즘

우선순위 큐의 핵심 연산은 크게 두 가지입니다.

  • Enqueue (삽입): 데이터와 함께 우선순위 정보를 저장합니다.
  • Dequeue (삭제): 저장된 데이터 중 우선순위가 가장 높은(또는 낮은) 요소를 찾아 제거하고 반환합니다.

2. 구현 방식 비교: 배열 vs 연결 리스트 vs 힙

우선순위 큐는 개념적인 정의(ADT)이므로, 이를 실제 코드로 구현하는 방법은 다양합니다. 배열이나 연결 리스트로도 구현할 수 있지만, 성능상의 이유로 대부분 힙(Heap)을 사용합니다. 각 구현 방식의 시간 복잡도를 비교하면 그 이유가 명확해집니다.

2-1. 배열(Array) 또는 연결 리스트(Linked List) 사용 시 문제점

  • 정렬되지 않은 배열: 삽입은 O(1)로 빠르지만, 삭제 시 가장 우선순위가 높은 데이터를 찾기 위해 전체를 탐색해야 하므로 O(n)이 소요됩니다.
  • 정렬된 배열: 삭제(꺼내기)는 O(1)로 빠르지만, 새로운 데이터를 삽입할 때마다 정렬 상태를 유지하기 위해 요소들을 이동시켜야 하므로 O(n)이 소요됩니다.

데이터가 많아질수록 O(n)의 성능은 시스템에 치명적인 부하를 줍니다. 따라서 삽입과 삭제 모두 균형 잡힌 성능을 보장하는 자료구조가 필요합니다.

3. 힙(Heap): 우선순위 큐를 위한 최적의 솔루션

힙(Heap)은 완전 이진 트리(Complete Binary Tree) 기반의 자료구조로, 최댓값이나 최솟값을 빠르게 찾아내도록 설계되었습니다. 힙은 우선순위 큐를 구현하기 위해 고안되었다고 해도 과언이 아닐 만큼 완벽한 파트너 관계를 가집니다.

3-1. 힙을 사용하는 기술적 이유 (Time Complexity)

힙을 사용할 경우 삽입과 삭제 연산의 시간 복잡도는 모두 O(log n)입니다. 이는 데이터가 1,000개일 때 약 10번, 100만 개일 때 약 20번의 연산만으로 처리가 가능함을 의미합니다. 배열을 사용했을 때의 O(n)과 비교하면 기하급수적인 성능 향상을 가져옵니다.

3-2. 힙의 종류와 특징

  • 최대 힙(Max Heap): 부모 노드의 키 값이 자식 노드보다 항상 크거나 같습니다. 루트 노드에는 가장 큰 값이 위치하므로 최대 우선순위 큐 구현에 적합합니다.
  • 최소 힙(Min Heap): 부모 노드의 키 값이 자식 노드보다 항상 작거나 같습니다. 루트 노드에는 가장 작은 값이 위치하므로 최소 우선순위 큐 구현에 적합합니다.

4. 파이썬(Python) `heapq` 모듈을 이용한 구현

파이썬은 내장 모듈 `heapq`를 통해 최소 힙(Min Heap) 기반의 우선순위 큐 기능을 제공합니다. 다음 코드는 우선순위 큐를 활용하여 데이터를 정렬하고 관리하는 예시입니다.


import heapq

class PriorityQueue:
    def __init__(self):
        self.heap = []

    def push(self, item, priority):
        # 튜플 형태로 (우선순위, 값)을 저장
        # heapq는 첫 번째 요소를 기준으로 정렬함
        heapq.heappush(self.heap, (priority, item))

    def pop(self):
        if not self.heap:
            return None
        # 우선순위가 가장 낮은(숫자가 작은) 요소 반환
        return heapq.heappop(self.heap)[1]

# 사용 예시
pq = PriorityQueue()
pq.push("작업 B", 2)  # 우선순위 2
pq.push("작업 A", 1)  # 우선순위 1 (가장 높음)
pq.push("작업 C", 3)  # 우선순위 3

print(pq.pop())  # "작업 A" 출력
print(pq.pop())  # "작업 B" 출력

위 코드에서 볼 수 있듯이, 힙을 이용하면 개발자는 복잡한 트리 구조를 직접 구현하지 않고도 효율적인 우선순위 관리가 가능합니다. 만약 최대 힙(Max Heap)이 필요하다면 우선순위 값에 음수(-)를 붙여 저장하는 팁을 활용할 수 있습니다.

[핵심 요약 : 우선순위 큐와 힙]
1. 개념: 들어온 순서가 아닌, 우선순위가 높은 데이터가 먼저 나가는 자료구조입니다.
2. 관계: 배열이나 연결 리스트보다 삽입/삭제 성능(O(log n))이 뛰어난 힙(Heap)으로 구현하는 것이 표준입니다.
3. 활용: 최단 경로 알고리즘(다익스트라), 스케줄링, 허프만 코딩 등 효율적인 최솟값/최댓값 관리가 필요한 모든 곳에 사용됩니다.

티스토리툴바